With the recent launch of the Cambridge Primary and Lower Secondary Mathematics curriculum frameworks there is much excitement around the introduction of the eight Thinking and Working Mathematics (TWM) characteristics. But what are they?
Thinking and working mathematically is a new feature in the Cambridge Primary and Lower Secondary Mathematics curriculum framework.
As with anything new, they will take a bit of time to become familiar with. To help, this blog is the first of three to support you in getting to know and understand each of the TWM characteristics.
Why have the 8 TWM characteristics been introduced?
The problem solving strand and problem solving learning objectives have been removed from the curriculum and replaced with TWM and the 8 TWM characteristics.
A question you might be thinking is, why have these characteristics been introduced?
The TWM characteristics are a way of explaining the mathematical processes that mathematicians use when solving problems. If students can use and apply these from Stage 1 onwards then they will be well-equipped to reason mathematically rather than just rote learn facts and figures.
To help you with this new aspect, whenever a question or activity in the Cambridge University Press series is linked to TWM, you will see this icon:
Problem solving and Thinking and Working Mathematically
Being able to solve problems is at the heart of doing mathematics. But being able to solve problems involves many skills and processes.
Depending on the complexity of a problem, all learners need scaffolds to support them to think and work mathematically. It is our job to provide these scaffolds using the 8 TWM characteristics.
The TWM characteristics assist teachers and learners to develop a toolkit of strategies to think and work mathematically, and solve problems efficiently and effectively.
Eight Thinking and Working Mathematics Characteristics
1. Specialising
Cambridge International’s definition: choosing an example and checking to see if it satisfies or does not satisfy specific mathematical criteria*.
Specialising is often a good place to begin thinking about a mathematical question. It means considering a simpler or familiar example. The act of specialising is not to get to an answer as such, but rather to pay attention to what you are doing in order to recognise any relationships that might appear.
Example
If 271 and 567 are added together, will the answer be odd or even
271 + 567 = an odd or even number?
I know that 271 and 567 are both odd numbers because the last digit is an odd number.
I can specialise using a simpler example, if I add 3 +3, will I get an odd or even answer?
3 + 3 = 6
So an odd number added to an odd number results in an even number.
2. Generalising
Cambridge International’s definition: recognising an underlying pattern by identifying many examples that satisfy the same mathematical criteria.
Generalising is the process of not focusing on one particular example, but rather trying to see a relationship among many.
Example
Let me use specialising again with another example:
5 + 7 = 12
Again, an odd number added to another odd number results in an even number. Let me try all odd numbers from 1 to 9.
Let me see if this is the same for 2 digit numbers and 3 digit numbers.
23 + 25 = 48, 309 + 453 = 562.
I conjecture that any odd number added to any other odd number always results in an even number. So, I think 271 + 567 will result in an even number. Let me do the calculation now or use a calculator to check if I am correct.
271
567
838
I was correct the answer is even.
By generalising (any) odd number + (any) odd number = even number.
3. Conjecturing
Cambridge International’s definition: forming mathematical questions or ideas.
Conjectures are thoughtful ideas or guesses – they might turn out to be untrue. Once a conjecture has been made, learners should try to justify it mathematically.
Example
I conjecture that when you multiply an even number by an odd number the answer will be an even number (this conjecture is correct).
Another student might conjecture that when you multiply an odd number by an odd number the answer will be even (this conjecture is incorrect).
A teacher would not confirm which conjecture is true, instead both students would use mathematical examples to show if there conjectures are correct.
4. Convincing
Cambridge International’s definition: presenting evidence to justify or challenge a mathematical idea or solution.
Developing mathematical reasoning involves trying to convince yourself and then someone else. It helps if the person you are trying to convince asks thoughtful questions. They should be convinced (or otherwise) through mathematical reasoning. The evidence presented can be simple (perhaps using equipment or drawings) or complex (using algebraic notation).
Example
I am going to convince myself that if I multiply 4 by 3 I get the product 12, which is even.
If I think of any even number as a and any odd number as a+1, then odd x even becomes a x (a+1) = 3a.
5. Characterising
Cambridge International’s definition: identifying and describing the mathematical properties of an object.
Learners often characterise mathematical shapes to find similarities and differences between them.
Example
Look for things that identify a kite:
A kite is a 2D shape with four straight sides. It has two pairs of equal-length sides that are adjacent to each other. The diagonals cross at right angles.
6. Classifying
Cambridge International’s definition: organising objects into groups according to their mathematical properties.
When we classify things, we sort them or group them based on similar characteristics.
Example
Sort these shapes by characteristics they have in common – square, kite, pentagon.
A square is a 2D shape with four equal straight sides. It has four angles that are all right angles.
A kite is a 2D shape with four straight sides. It has two pairs of equal-length sides that are adjacent to each other. The diagonals cross at right angles.
I classify kites and squares into one group – quadrilaterals – because they have four sides and four angles.
7. Critiquing
Cambridge International’s definition: comparing and evaluating mathematical ideas, representations or solutions to identify advantages and disadvantages.
When we critique mathematical ideas or solutions, we are reflecting on what we can see. It also offers the opportunity to consider and discuss alternative viewpoints. Critiquing offers students the opportunity to think harder.
Example
With this example, the number line is a better representation of 1/3 than the bar model because it shows the ordinal value of the fraction.

8. Improving
Cambridge International’s definition: refining mathematical ideas or representations to develop a more effective approach or solution.
We can all improve and so it is an important characteristic to be able to reflect, refine and develop our mathematical ideas and solutions based on critiquing by ourselves or others to find more elegant solutions.
Example
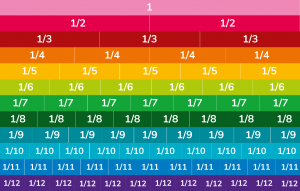
Fraction walls really help to see how fractions with different denominators are connected to each other.
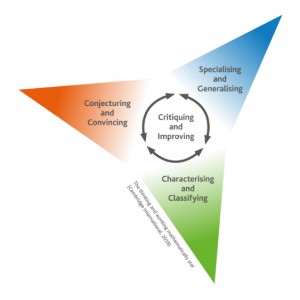
Four pairs of Thinking and Working Mathematics characteristics
- Specialising and Generalising
- Conjecturing and Convincing
- Characterising and Classifying
- Critiquing and Improving
You will notice that the eight characteristics are grouped together as four pairs. Each pair of characteristics works together and complements each other.
However, you do not have to teach the pairs of characteristics together, you can mix and match in one lesson. For example, you may find that you are creating some lessons that draw on conjecturing and improving.
Summary
This blog gives you an insight into the TWM characteristics and hopefully you’re now feeling prepared and excited to bring them into your maths lessons. If you are looking for more support, the Cambridge University Press revised Primary and Lower Secondary mathematics series supports the 8 TWM characteristics, just look for the activities with the star by them.
To learn more about how the Cambridge University Press primary and lower secondary series, go to the hub page.
*Note: TWM definitions are from the Cambridge Assessment International Education Primary and Lower Secondary Mathematics curriculum materials.



